[無料ダウンロード! √] 連立 方程式 中学2年生 数学 294256
< 中学校数学 2年生/数量 目次 1 連立方程式とは何か 2 連立方程式の解き方 21 加減法 22 代入法 3 いろいろな連立方程式の解法 31 カッコのある連立方程式 32 分数や小数のある連立方程式 33 分母に文字がある連立方程式 34 A=B=C の形の連立方程式 35 3元1次方程式 4 連立方程式の利用 連立方程式とは何か まず、この問題を考えてみてほしい。 例題1 一本30円の鉛筆と一個50円の消しゴムを
連立 方程式 中学2年生 数学-2年 連立方程式 解と係数 (1)問題, (3)答b=5(誤) b=3(正) 1年 1,2年生で(発展)と書いてある問題は少し難易度が高くなっています。また、3年生では(基礎)と書いてある問題以外は難易度を高くした問題が含まれます。 中学校数学学習サイト 中学数学2つの式から連立方程式を作ると $$\begin{eqnarray} \left\{ \begin{array}{l} 15x 15y = 3600 \\ 30x – 30y = 3600 \end{array} \right \end{eqnarray}$$ あとは、この方程式を解いていくだけです。 係数を揃えて、加減法で解いていきます。 $$30x30y=70$$ $$30x30y=3600$$ それぞれの式を足すと
連立 方程式 中学2年生 数学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | 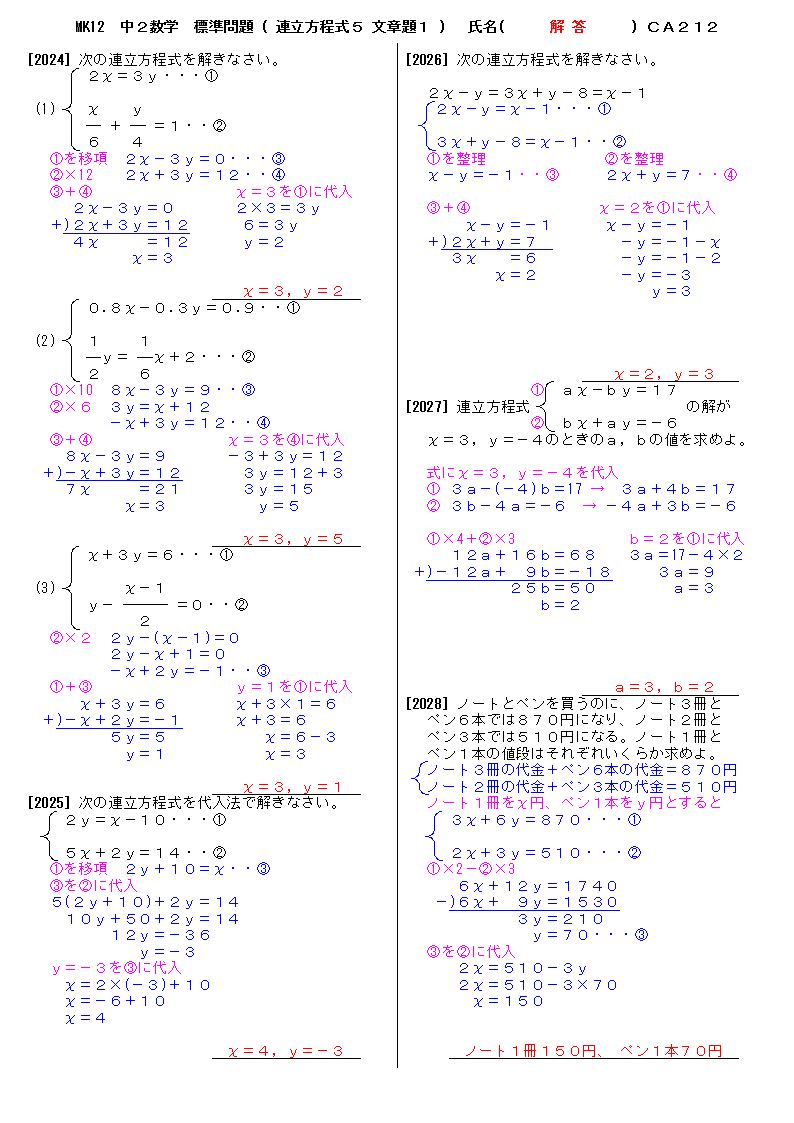 |
 |  |  |
 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
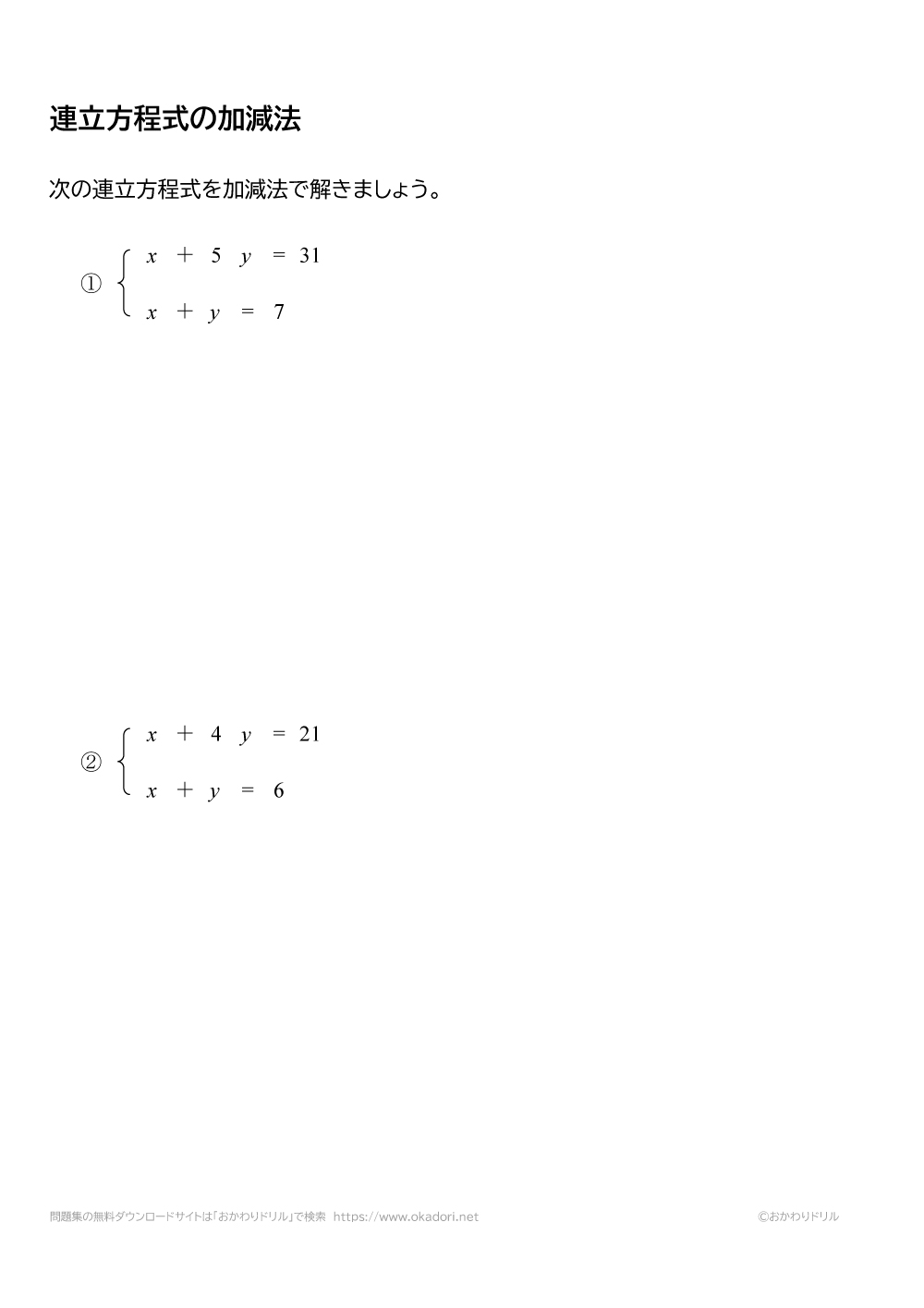 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 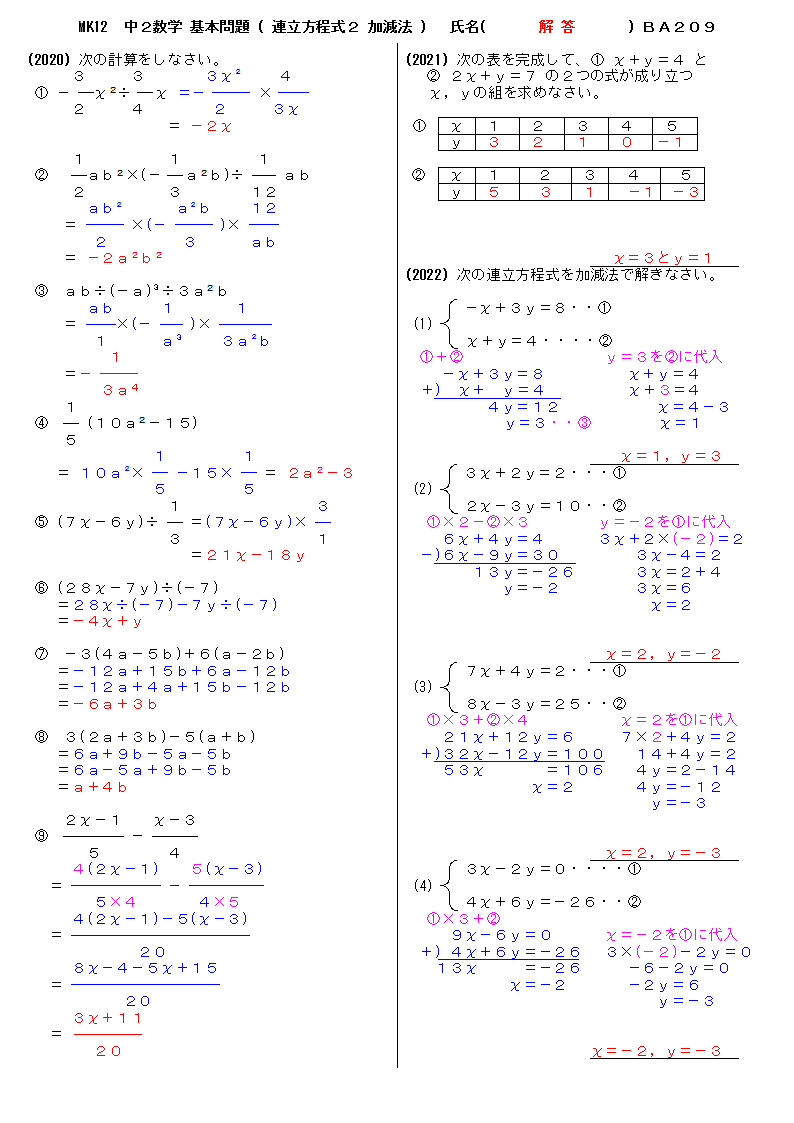 |  |
 |  |  |
 |  |  |
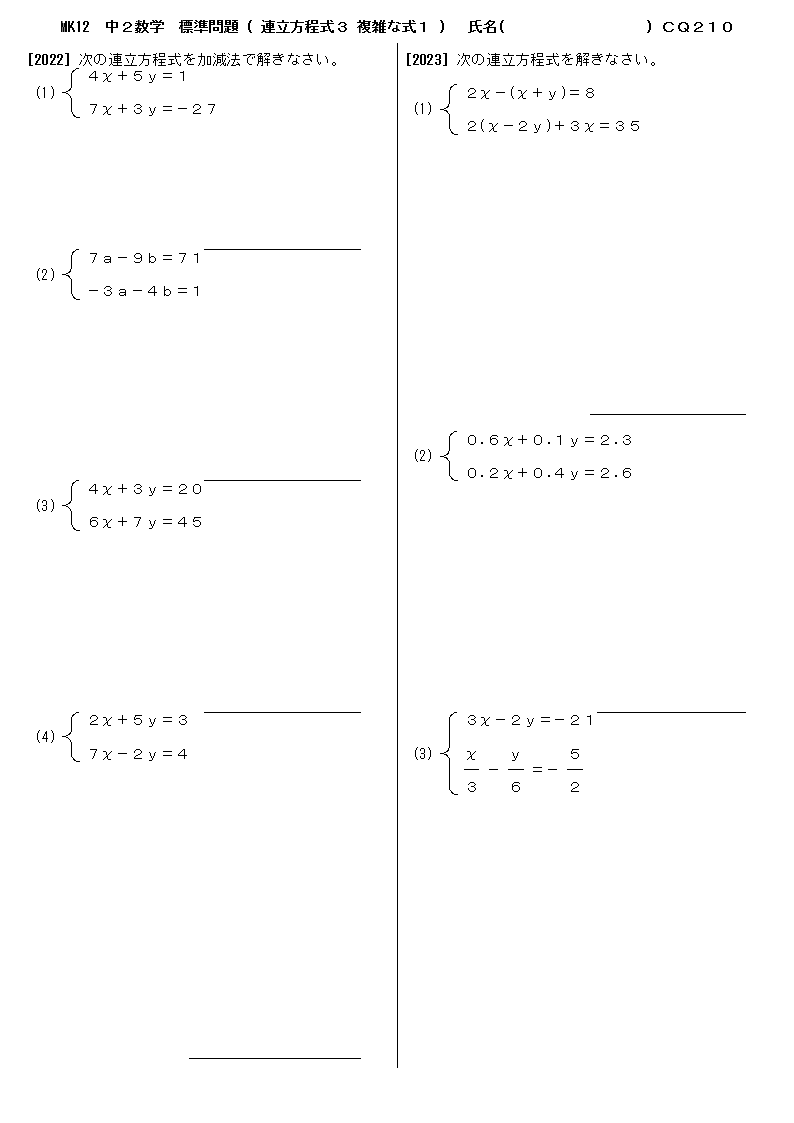 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 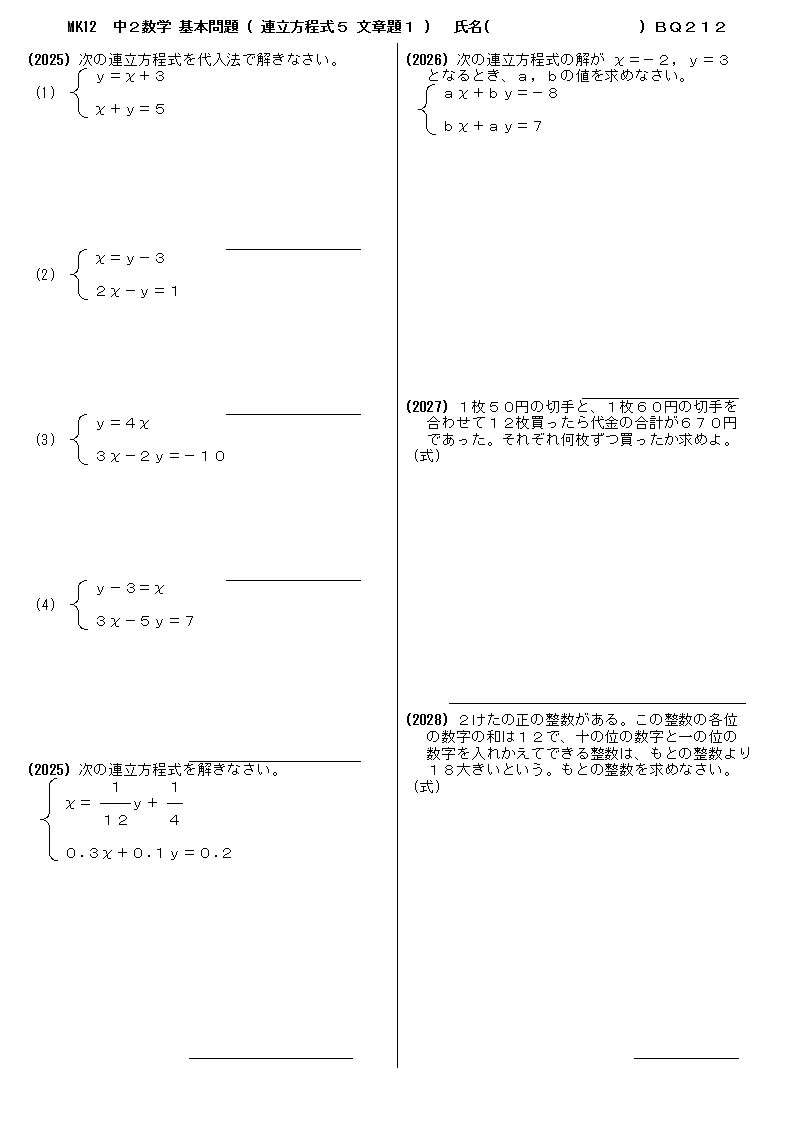 |  |
 |  |  |
 |  | |
 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
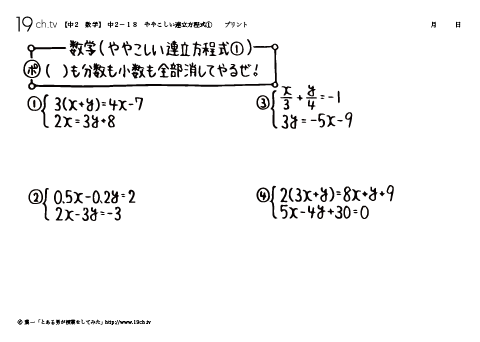 |  |  |
 |  |  |
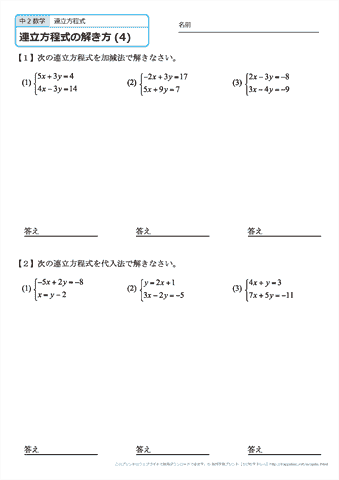 |  | |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 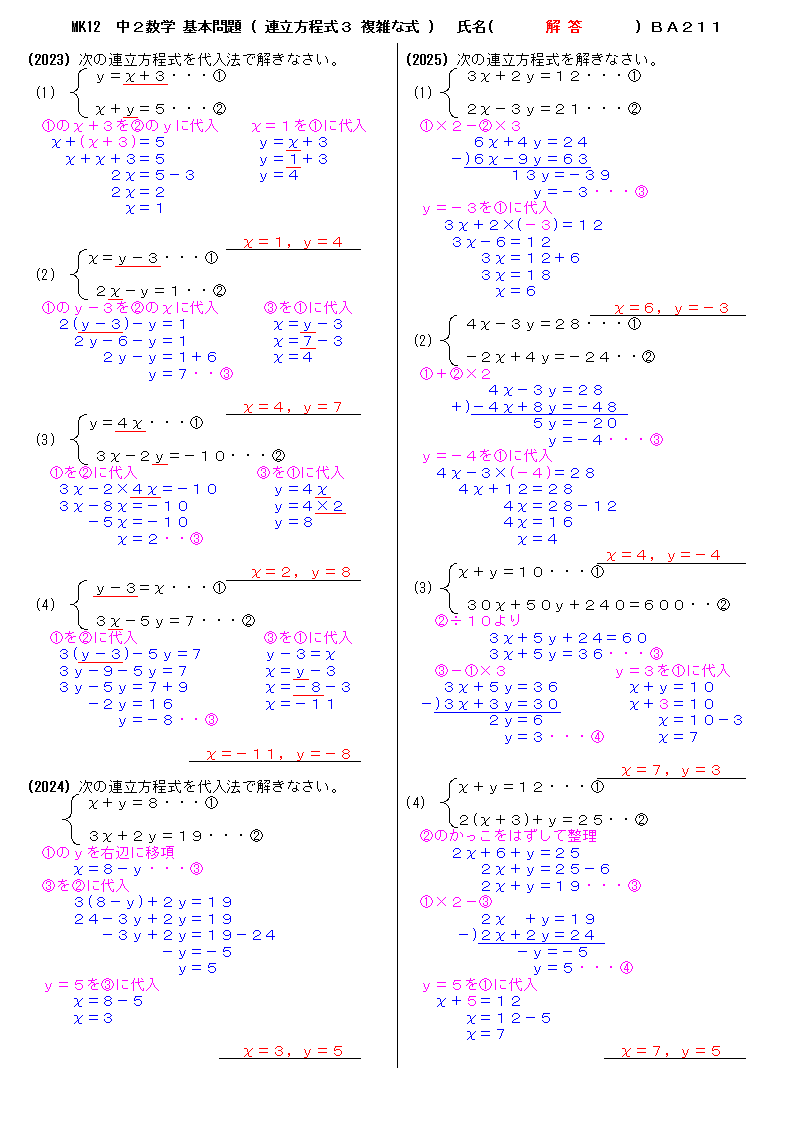 |  |
 |  |  |
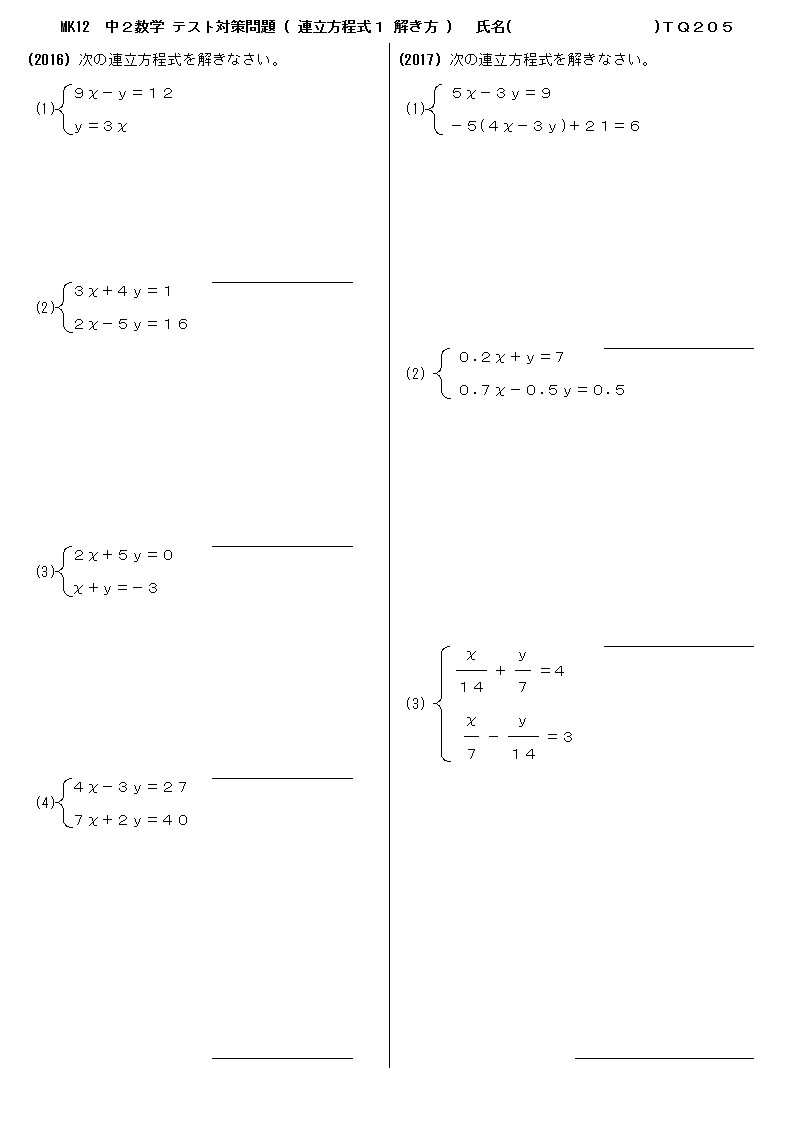 |  |  |
「連立 方程式 中学2年生 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |
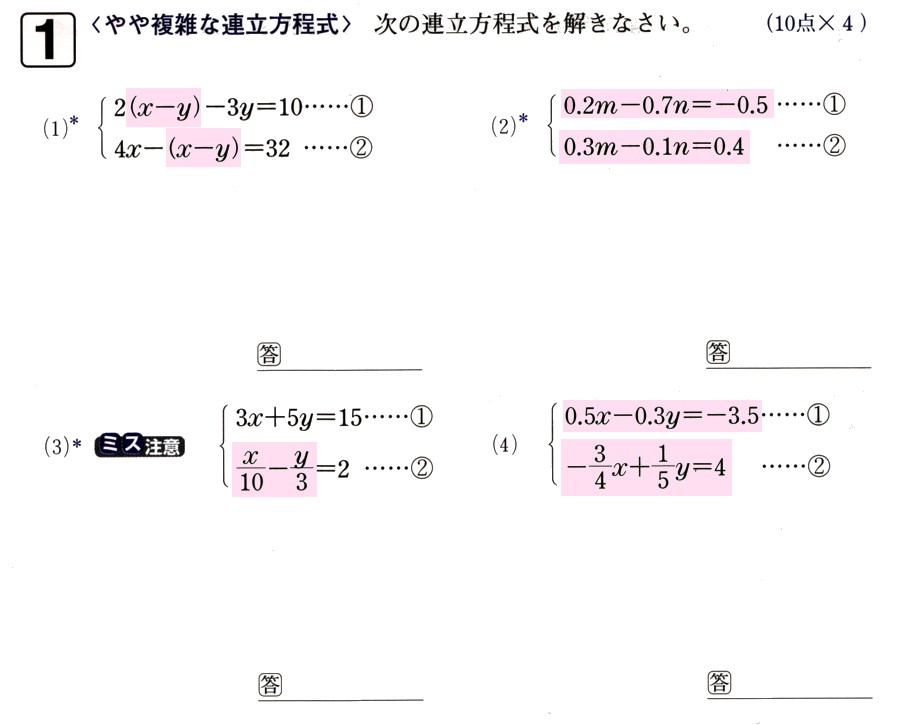
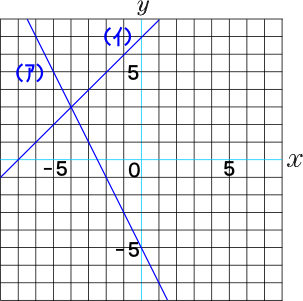
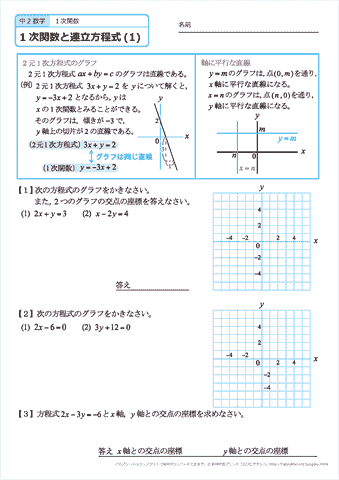
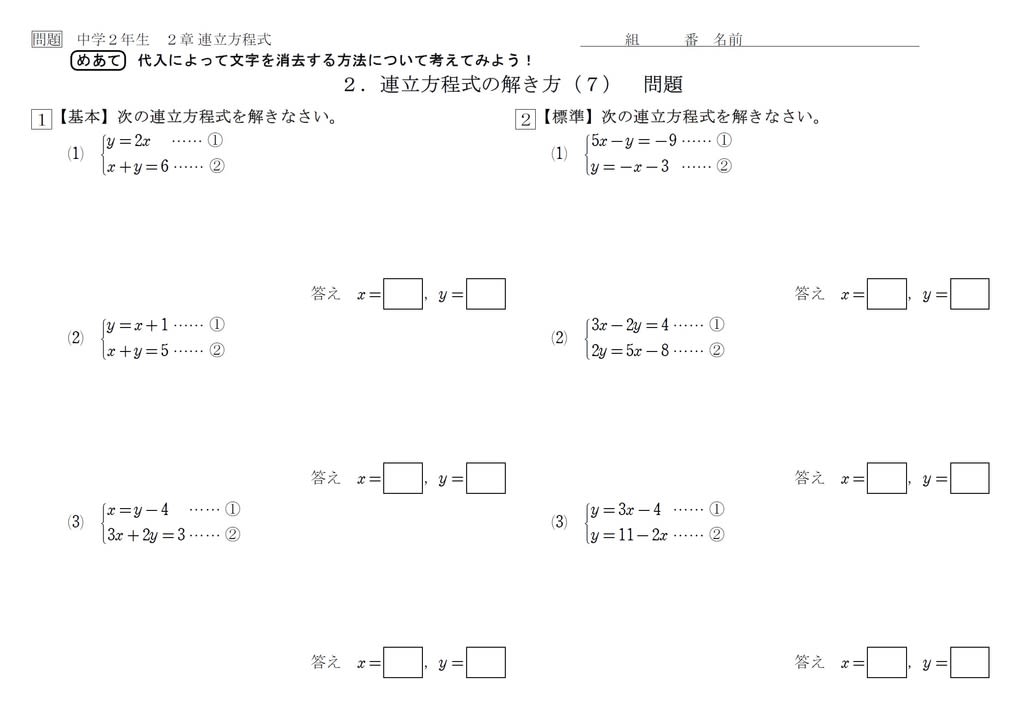
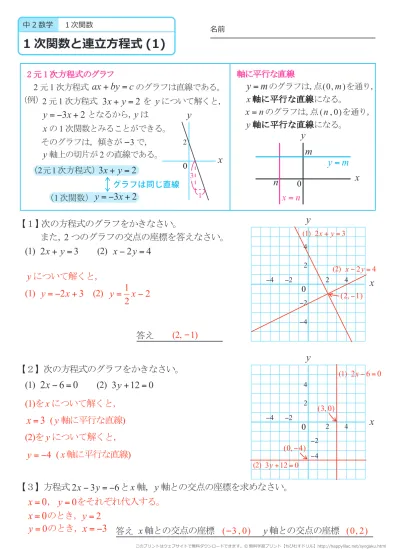
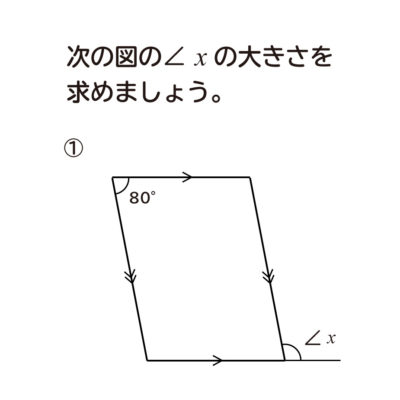
中学校2年生数学 WEB問題(チャレンジシート) 中学校2年生 数学科 ①式の計算 ① 問題 解答 ②連立方程式 ① 問題 解答「連立方程式を解く」とは → 同じ未知数 (x, yなど)についての方程式が2つ以上あるとき、それらすべてを 同時に満たす 未知数の値を決定すること ですね 簡単にいえば → それぞれ無数の解を持つ方程式達の 共通解 を求めることですね (関数的に言えば、 交点 を求めること) ① 連立方程式の解法 連立方程式 難しくはありません! 式が2つあるだけです (正確には、ここでは二元一次方程式が2つある
コメント
コメントを投稿